2  Introducción a la ciencia de datos

En este capítulo se definen algunos conceptos fundamentales de estadística, como observaciones y variables. También se introduce el área de conocimiento denominada ciencia de datos.

2.1 Resumen

Una investigación estadística se basa en datos. Los datos acostumbran representarse en tablas, en las cuales cada fila es una observación y cada columna es una variable. Una observación corresponde a un elemento de datos que ha sido estudiado y cada variable a una característica de ese elemento de datos. Las variables pueden ser numéricas o categóricas. Las numéricas se subdividen en discretas y continuas y las categóricas en nominales y ordinales.

La ciencia de datos es una disciplina que permite convertir datos “crudos” en comprensión y conocimiento. Incluye los procesos importar, ordenar, transformar, visualizar, modelar y comunicar.

2.2 Trabajo previo

2.2.1 Lecturas

Çetinkaya-Rundel, Mine, & Hardin, Johanna (2021). Introduction to Modern Statistics (1st ed.). OpenIntro, Inc. https://openintro-ims.netlify.app/ (capítulo 1)

Wickham, Hadley; Çetinkaya-Rundel, Mirne; & Grolemund, Garret (2023). R for Data Science: Import, Tidy, Transform, Visualize, and Model Data (2nd ed.). O’Reilly Media. https://r4ds.hadley.nz/ (capítulo introductorio)

2.3 Datos

Los científicos tratan de responder preguntas mediante métodos rigurosos y observaciones cuidadosas. Estas observaciones, recopiladas de notas de campo, encuestas y experimentos, entre otras fuentes, forman la columna vertebral de una investigación estadística y se denominan datos. La presentación y descripción efectivas de los datos constituyen el primer paso en un análisis (Çetinkaya-Rundel & Hardin, 2021). Esta sección introduce una estructura para organizar los datos, así como alguna terminología que se utilizará a lo largo de este curso.

2.3.1 Observaciones y variables

La siguiente tabla contiene 10 filas de un conjunto de datos. Cada fila corresponde a una persona y cada columna a una característica de esa persona. En términos estadísticos, cada fila es una observación y cada columna es una variable.

Conjunto de datos de personas.
id provincia equipo masa estatura sexo cantidad_hermanos nivel_guitarra
1 Limón Saprissa 51.0 1.51 mujer 0 nulo
2 Heredia Herediano 98.5 1.87 hombre 1 alto
3 Guanacaste Liberia 91.6 1.65 mujer 4 bajo
4 Limón Liberia 60.6 1.68 mujer 1 alto
5 Cartago Cartaginés 59.1 1.73 mujer 3 bajo
6 otra San Carlos 59.2 1.89 hombre 3 bajo
7 Guanacaste Cartaginés 65.2 1.70 mujer 3 alto
8 Guanacaste Sporting 76.2 1.76 hombre 3 experto
9 Limón Alajuelense 71.6 1.80 hombre 4 bajo
10 Alajuela Alajuelense 64.6 1.52 hombre 2 bajo

2.3.2 Tipos de variables

Los datos de la tabla 2.1. son de varios tipos, cuya jerarquía se muestra en la Figura 2.1.

flowchart TB
    A["Todas las variables"] --> B["Numéricas"]
    A --> C["Categóricas"]
    B --> D["Discretas"]
    B --> E["Continuas"]
    C --> F["Ordinales"]
    C --> G["Nominales"]
Figura 2.1: Tipos de variables estadísticas.

2.3.2.1 Numéricas

Corresponden a números. Se les pueden aplicar operaciones como suma, resta, multiplicación, división y otras similares.

2.3.2.1.1 Discretas

Toman valores específicos que se pueden contar. La variable cantidad_hermanos es discreta. Existe una separación clara entre sus posibles valores. Por ejemplo, es posible tener 1, 2 o 3 hermanos, pero no es posible tener 2.5 hermanos.

2.3.2.1.2 Continuas

Pueden tomar cualquier valor dentro de un intervalo o rango continuo. Estas variables se caracterizan por su capacidad para representar medidas precisas y pueden asumir un número infinito de valores, incluso dentro de un rango limitado (ej. entre 0 y 1). Las variables masa y estatura son continuas.

2.3.2.2 Categóricas

Las variables categóricas (también llamadas cualitativas), son aquellas que describen una característica o cualidad de una observación y clasifican las observaciones en grupos o categorías. A diferencia de las variables numéricas, que expresan cantidades numéricas, las variables categóricas expresan atributos no numéricos.

2.3.2.2.1 Nominales

No existe un orden inherente o jerarquía entre las categorías. Las variables provincia, equipo y sexo son nominales.

2.3.2.2.2 Ordinales

Hay un orden o jerarquía clara entre las categorías. La variable nivel_guitarra es categórica.

Ejercicio
Si se agregaran las siguientes variables al conjunto de datos de personas mostrado anteriormente, ¿cuál sería su tipo (discreta, continua, ordinal, nominal)?:

  • Cédula de identidad.
  • Número de teléfono.
  • Fecha de nacimiento.
  • Ubicación de la residencia.

2.4 Ciencia de datos

La ciencia de datos es una disciplina que permite convertir datos “crudos” en comprensión y conocimiento (Wickham, Çetinkaya-Rundel, & Grolemund, 2023). Utiliza estadística y ciencias de la computación, entre otras disciplinas.

2.4.1 Procesos

La Figura 2.2 ilustra el modelo de un proyecto típico de ciencia de datos, el cual incluye los procesos de importar, ordenar, transformar, visualizar, modelar y comunicar. Todos se articulan mediante programación de computadoras.

  • Importar los datos típicamente implica leerlos de un archivo, una base de datos o una interfaz de programación de aplicaciones (API) y cargarlos en un data frame.

  • Ordenar u organizar (tidy) los datos significa colocarlos en estructuras rectangulares de filas y columnas, similares a tablas, de manera que cada fila sea una observación y cada columna una variable.

  • Transformar los datos implica la generación de algún subconjunto de filas y columnas, la creación de nuevas variables o el cálculo de estadísticas (ej. conteos, promedios, mínimos, máximos).

  • Visualizar los datos (en tablas, gráficos, mapas, etc.) permite encontrar patrones inesperados o formular nuevas preguntas.

  • Modelar es crear una representación abstracta y estructurada de los datos, con el fin de facilitar su análisis y realizar predicciones.

  • Comunicar es el último paso y es una actividad crítica de cualquier proyecto de análisis de datos o de ciencia en general.

2.4.2 Ejemplo

Se ejemplifica el proceso de ciencia de datos mediante el conjunto de datos NHANES (National Health and Nutrition Examination Survey, Encuesta Nacional de Salud y Nutrición), recopilado por el US National Center for Health Statistics (NHCS, Centro Nacional de Estadísticas de Salud de Estados Unidos), como parte de un programa de estudios diseñado para evaluar el estado de salud y nutrición de adultos y niños en los Estados Unidos. El programa NHANES selecciona muestras representativas de la población estadounidense y recopila información a través de cuestionarios, exámenes médicos y pruebas de laboratorio.

El conjunto de datos consta de 20293 observaciones (personas) y 78 variables de diferentes clases: antropométricas (ej. peso, altura, IMC), demográficas (ej. edad, sexo, nivel educativo, estado civil), de salud (ej. tensión arterial, estado de salud general, hábitos de consumo de tabaco) y socioeconómicas (ej. ingresos, número de habitaciones en la vivienda).

A continuación, se muestra como los procesos de ciencia de datos, aplicados en el conjunto de datos NHANES, pueden implementarse en el lenguaje de programación R.

2.4.2.1 Importar

El conjunto de datos se importa desde un archivo de valores separados por comas (CSV) ubicado en https://raw.githubusercontent.com/gf0604-procesamientodatosgeograficos/2025-i/refs/heads/main/datos/nchs/nhanes.csv.

Código 
# Importar los datos desde un archivo CSV
nhanes <- read.csv(
  "https://raw.githubusercontent.com/gf0604-procesamientodatosgeograficos/2025-i/refs/heads/main/datos/nchs/nhanes.csv"
)

# Desplegar el conjunto de datos
datatable(
  nhanes,
  caption = "Conjunto de datos NHANES completo",
  rownames = FALSE,
  options = list(
    pageLength = 5,
    language = list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Spanish.json')
  )    
)

Ejercicio
Descargue el archivo CSV del conjunto de datos NHANES de https://raw.githubusercontent.com/gf0604-procesamientodatosgeograficos/2025-i/refs/heads/main/datos/nchs/nhanes.csv y examínelo con un programa de hoja de cálculo (ej. Excel, Calc). Observe las diferentes variables y sus tipos de datos.

2.4.2.2 Ordenar (tidy)

En este caso, los datos están bien organizados en una estructura rectangular de filas y columnas, en la que cada fila es una observación y cada columna una variable, por lo que no es necesaria una reorganización profunda de los datos. Sin embargo, para facilitar el procesamiento, se conservan solo las columnas que son de interés y se elimina el resto.

Código 
# Seleccionar columnas de interés
nhanes <- 
  nhanes[, c("ID", "Gender", "Age", "Race3", "Weight", "Height", "Depressed")]

# Desplegar el conjunto de datos
datatable(
  nhanes,
  caption = "Conjunto de datos NHANES con columnas seleccionadas.",
  rownames = FALSE,
  options = list(
    pageLength = 5,
    language = list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Spanish.json')
  )    
)

2.4.2.3 Transformar

El proceso de transformación se ilustra mediante dos ejemplos.

2.4.2.3.1 Promedio de estatura de personas adultas por sexo

Para comparar las estaturas de hombres y mujeres adultos, el conjunto de datos se transforma con dos operaciones:

  1. Se filtra por edad (Age >= 18).
  2. Se agrupa por sexo y para cada valor ("female","male") se calcula el promedio de estatura.

Además, la estatura (expresada en cm) se redondea a dos posiciones decimales para facilitar la lectura.

Código 
# Filtrar adultos
nhanes_adultos <- subset(nhanes, Age >= 18)

# Calcular el promedio de estatura por sexo
nhanes_promedio_estatura_x_sexo_adultos <- aggregate(
  data = nhanes_adultos, 
  Height ~ Gender, 
  FUN = mean, 
  na.rm = TRUE
)

# Ordenar descendentemente por estatura
nhanes_promedio_estatura_x_sexo_adultos <- 
  nhanes_promedio_estatura_x_sexo_adultos[order(-nhanes_promedio_estatura_x_sexo_adultos$Height), ]

# Redondear la estatura a 2 decimales
nhanes_promedio_estatura_x_sexo_adultos$Height <- round(
  nhanes_promedio_estatura_x_sexo_adultos$Height, 
  2
)

# Desplegar el conjunto de datos
datatable(
  nhanes_promedio_estatura_x_sexo_adultos,
  caption = "Promedio de estatura (cm) por sexo.",
  rownames = FALSE,
  options = list(
    paging = FALSE,
    searching = FALSE,
    info = FALSE,
    language = list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Spanish.json')
  )    
)
2.4.2.3.2 Promedio de peso de personas adultas por grupo étnico

El conjunto de datos se transforma con tres operaciones:

  1. Se filtra por edad (Age >= 18).
  2. Se agrupa por grupo étnico y para cada valor ("Black", "Hispanic", "Asian", etc.) se calcula el promedio de peso.
  3. Se ordena descendentemente por peso.

Además, el peso (expresado en kg) se redondea a dos posiciones decimales para facilitar la lectura.

Código 
# Filtrar adultos
nhanes_adultos <- subset(nhanes, Age >= 18)

# Calcular el promedio de peso por grupo étnico
nhanes_promedio_peso_x_etnia_adultos <- aggregate(
  data = nhanes_adultos, 
  Weight ~ Race3, 
  FUN = mean, 
  na.rm = TRUE
)

# Ordenar descendentemente por peso
nhanes_promedio_peso_x_etnia_adultos <- 
  nhanes_promedio_peso_x_etnia_adultos[order(-nhanes_promedio_peso_x_etnia_adultos$Weight), ]


# Redondear el peso a 2 decimales
nhanes_promedio_peso_x_etnia_adultos$Weight <- round(
  nhanes_promedio_peso_x_etnia_adultos$Weight, 
  2
)

# Desplegar el conjunto de datos
datatable(
  nhanes_promedio_peso_x_etnia_adultos,
  caption = "Promedio de peso (kg) por grupo étnico.",
  rownames = FALSE,
  options = list(
    paging = FALSE,
    searching = FALSE,
    info = FALSE,
    language = list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Spanish.json')
  )    
)

2.4.2.4 Visualizar

Se presentan tres ejemplos de visualizaciones.

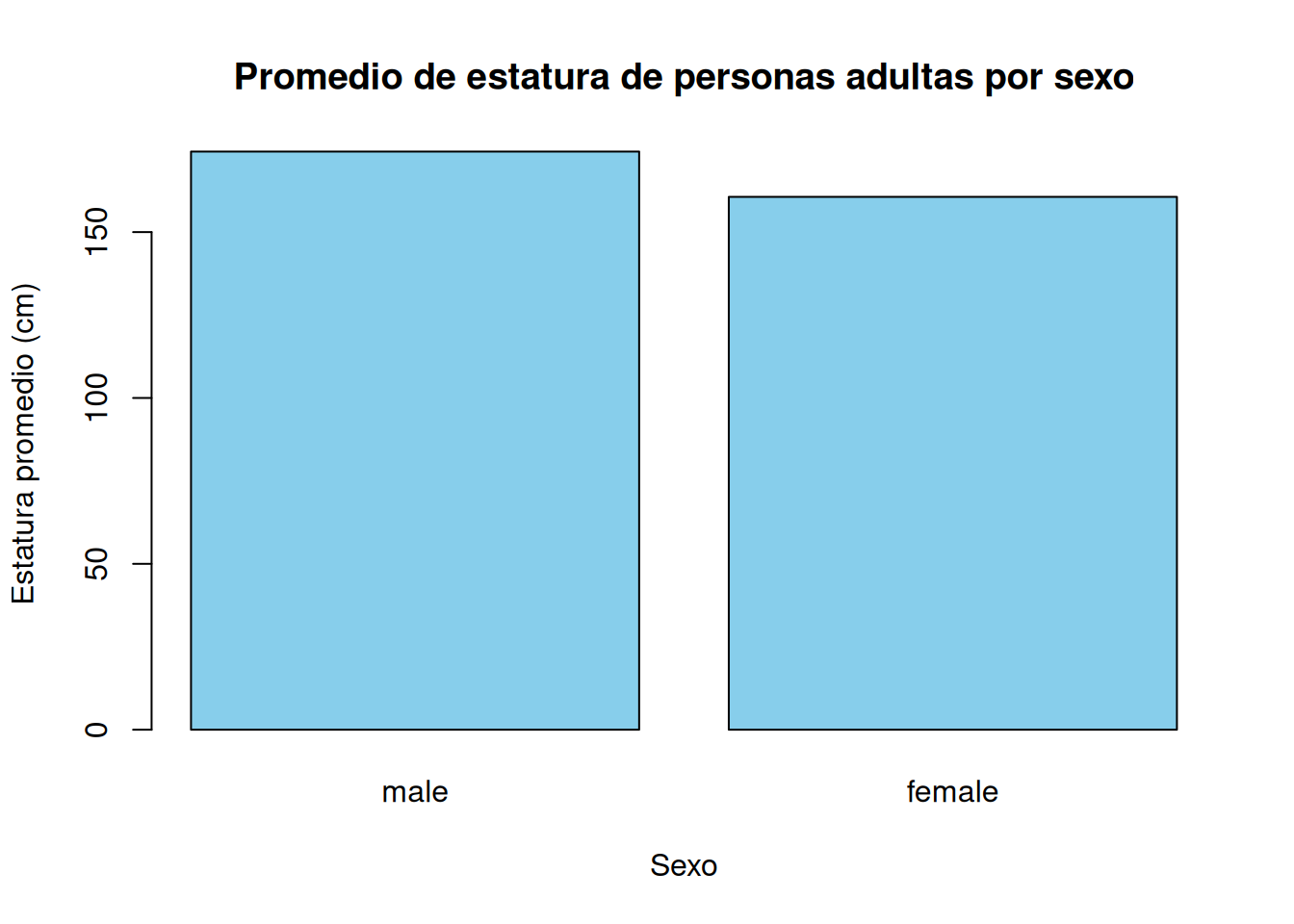
2.4.2.4.1 Promedio de estatura de personas adultas por sexo
Código 
# Gráfico de barras
barplot(
  nhanes_promedio_estatura_x_sexo_adultos$Height, 
  names.arg = nhanes_promedio_estatura_x_sexo_adultos$Gender, 
  col = "skyblue", 
  main = "Promedio de estatura de personas adultas por sexo",
  xlab = "Sexo",
  ylab = "Estatura promedio (cm)",
  las = 0
)

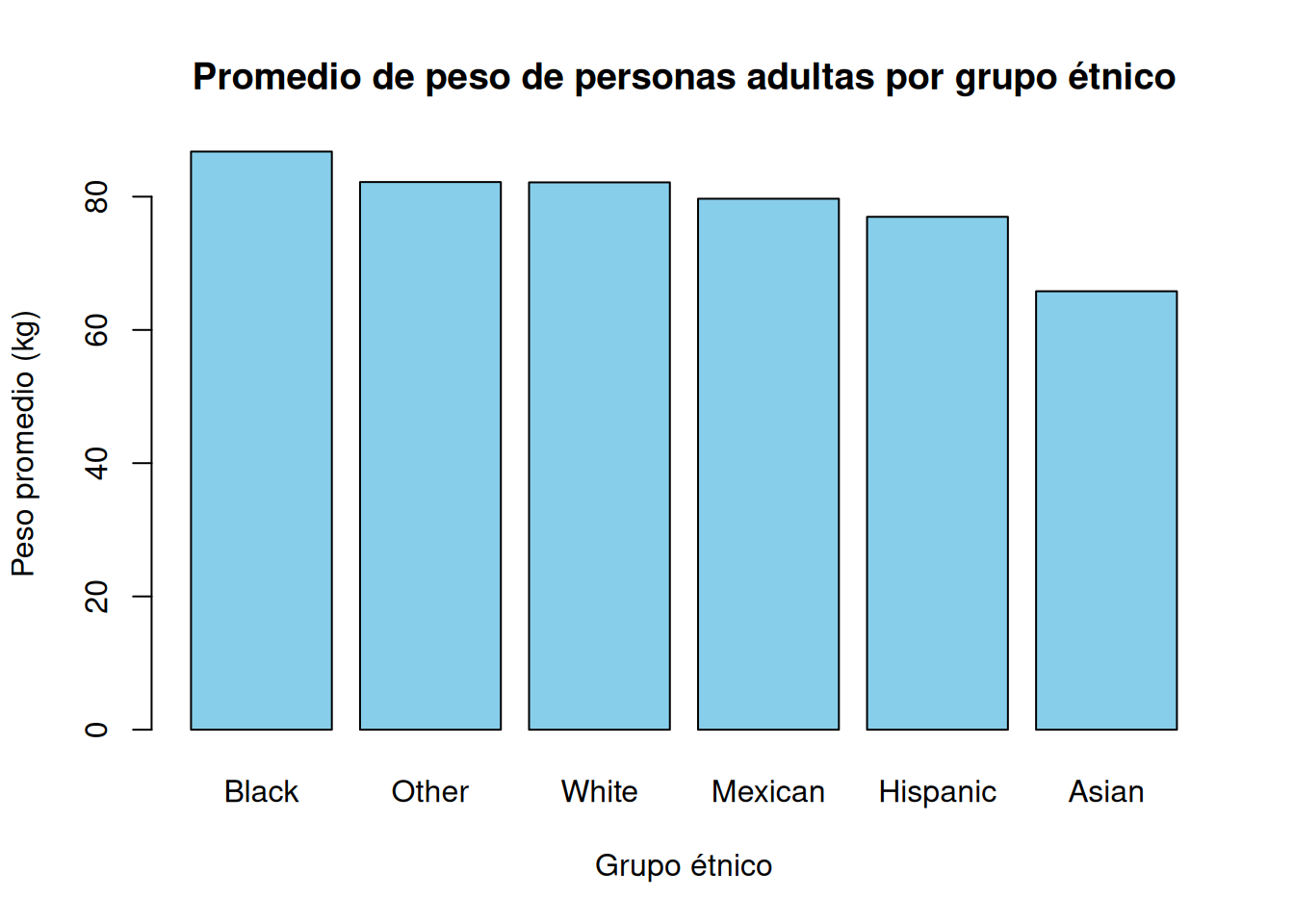
2.4.2.4.2 Promedio de peso de personas adultas por grupo étnico
Código 
# Gráfico de barras
barplot(
  nhanes_promedio_peso_x_etnia_adultos$Weight,
  names.arg = nhanes_promedio_peso_x_etnia_adultos$Race3, 
  col = "skyblue", 
  main = "Promedio de peso de personas adultas por grupo étnico",
  xlab = "Grupo étnico",
  ylab = "Peso promedio (kg)",
  las = 0
)

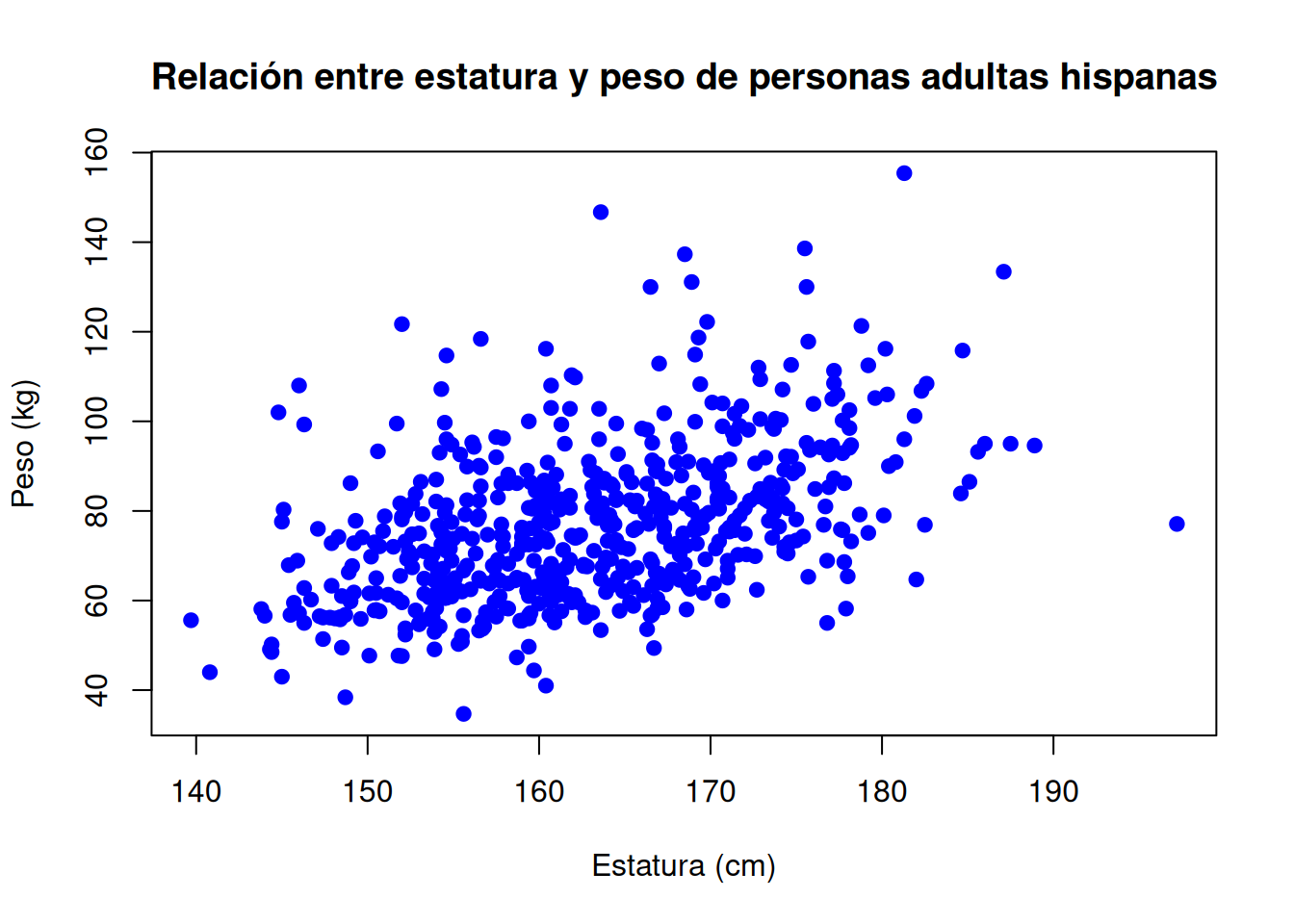
2.4.2.4.3 Relación entre estatura y peso de personas adultas hispanas
Código 
# Subconjunto de personas adultas hispanas
nhanes_adultos_hispanos <- subset(nhanes_adultos, Race3 == "Hispanic")

# Gráfico de dispersión
plot(
  nhanes_adultos_hispanos$Height,
  nhanes_adultos_hispanos$Weight,
  main = "Relación entre estatura y peso de personas adultas hispanas", 
  xlab = "Estatura (cm)",
  ylab = "Peso (kg)",
  pch = 19,
  col = "blue"
)

2.4.2.5 Modelar

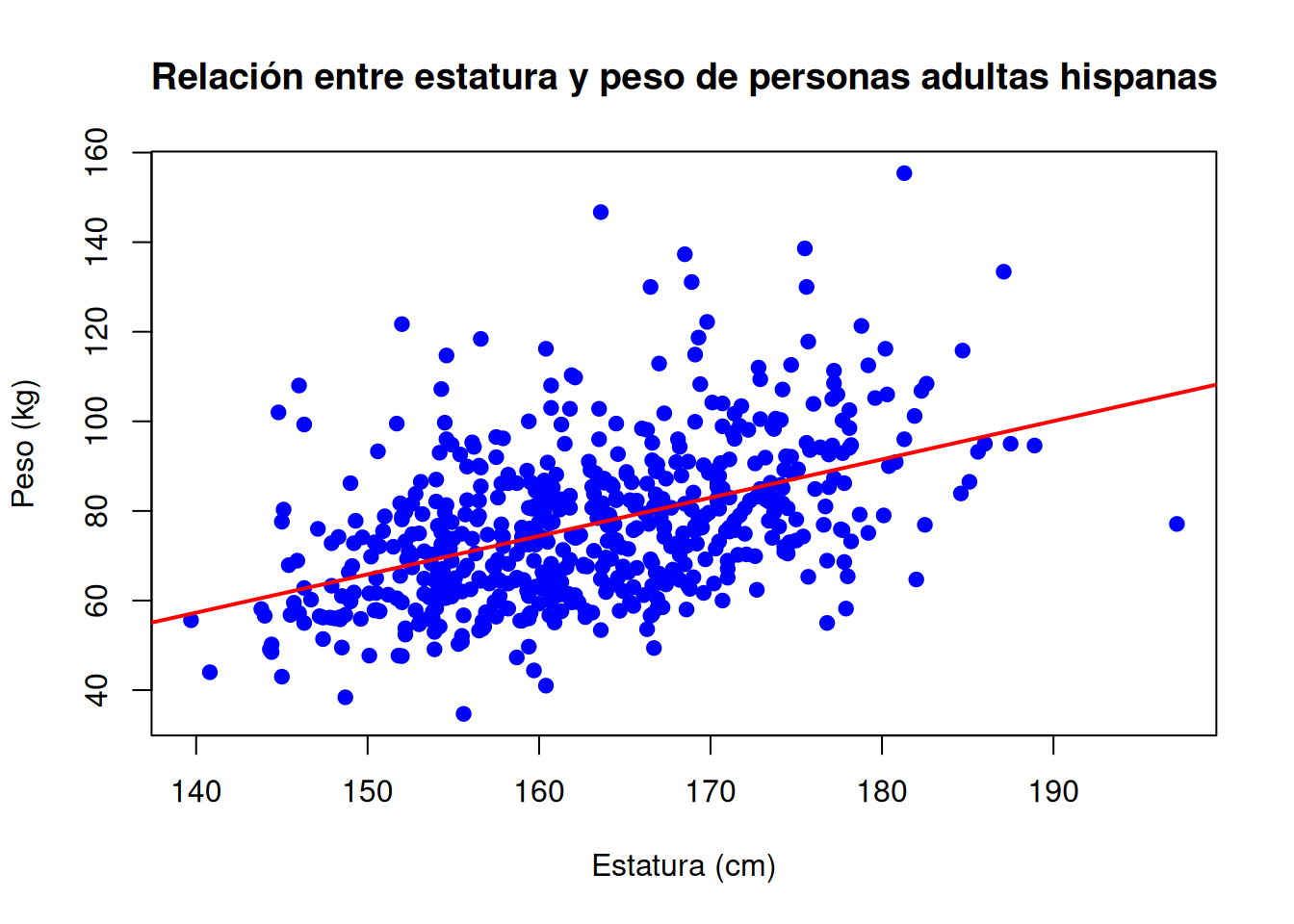
2.4.2.5.1 Predicción del peso a partir de la estatura en personas adultas hispanas

El proceso de modelar se ilustra mediante un modelo de regresión lineal.

Código 
# Ajustar el modelo de regresión
modelo_peso_estatura <- lm(Weight ~ Height, data = nhanes_adultos_hispanos)

# Gráfico de dispersión
plot(
  nhanes_adultos_hispanos$Height,
  nhanes_adultos_hispanos$Weight,
  main = "Relación entre estatura y peso de personas adultas hispanas", 
  xlab = "Estatura (cm)",
  ylab = "Peso (kg)",
  pch = 19,
  col = "blue"
)

# Línea de tendencia del modelo
abline(
  modelo_peso_estatura,
  col = "red",
  lwd = 2
)

El siguiente es un resumen estadístico del modelo.

Código 
# Desplegar un resumen estadístico del modelo
summary(modelo_peso_estatura)

Call:
lm(formula = Weight ~ Height, data = nhanes_adultos_hispanos)

Residuals:
    Min      1Q  Median      3Q     Max 
-35.945 -10.921  -1.856   8.031  69.213 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -62.43629   11.16381  -5.593 3.46e-08 ***
Height        0.85528    0.06838  12.509  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15.5 on 573 degrees of freedom
  (41 observations deleted due to missingness)
Multiple R-squared:  0.2145,    Adjusted R-squared:  0.2131 
F-statistic: 156.5 on 1 and 573 DF,  p-value: < 2.2e-16

Este resumen nos dice que la estatura es un predictor significativo del peso, pero el modelo deja mucha variación sin explicar. Para una mejor predicción, se podría considerar añadir otras variables (edad, sexo, condición física, etc.).

Podemos utilizar el modelo para predecir estaturas de personas adultas hispanas a partir de su peso.

Código 
# Ejemplo de predicciones para nuevas alturas
nuevas_estaturas <- data.frame(Height = c(150, 160, 170))
predicciones <- predict(modelo_peso_estatura, newdata = nuevas_estaturas)

# Mostrar las predicciones
data.frame(
  Estatura = nuevas_estaturas$Height,
  Peso_predicho = round(predicciones, 2)
)
  Estatura Peso_predicho
1      150         65.86
2      160         74.41
3      170         82.96

2.4.2.6 Comunicar

La comunicación puede realizarse de muchas maneras. Por ejemplo, a través de una página web desarrollada en Quarto, que incluya los datos, el código fuente y los resultados, como es el caso de este documento.

2.5 Referencias

Çetinkaya-Rundel, M., & Hardin, J. (2021). Introduction to Modern Statistics (1st ed.). OpenIntro, Inc. Retrieved from https://openintro-ims.netlify.app/
Wickham, H., Çetinkaya-Rundel, M., & Grolemund, G. (2023). R for Data Science: Import, Tidy, Transform, Visualize, and Model Data (2nd ed.). O’Reilly Media. Retrieved from https://r4ds.hadley.nz/